For the past few months, I've been implementing machine learning algorithms and one of the small details about higher dimensional spheres caught me by surprise.
Back in Real Analysis, every student goes through solving for the volume of a n-Dimensional sphere and gets:
where \(r\) is the radius, \(n\) is the dimension, and \(\Gamma\) is the Gamma Function. Even without knowing the above equation, it is natural to assume that \(V_n(r)\) is proportional to \(r^n\) or \(V_n(r)=Ar^n\), where \(A\) is a constant.
To make this example more concrete, lets say we want to find the fraction of the volume of a sphere of radius, \(R\), that lies between \(r=0.95R\) and \(r=R\). In other words, we want to find the fractional volume of the blue region:
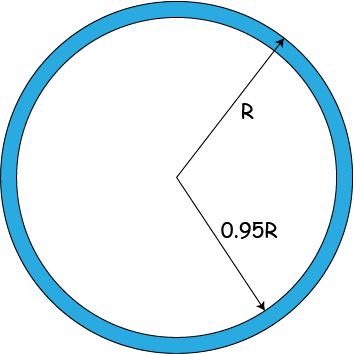
Using basic algebra the fractional volume is:
where \(f\) is fractional volume. As the dimension, N, increases the fractional volume tends to one, as shown in this table:

In other words, in higher dimensions, almost all the volume of the sphere is in the shell that has a thickness equal to 5% of the radius. Mind-blowing?